

|
||
| GBB Services | ||
| GBB Services : Mathematics : cos2+sin2=1 |
Different ways of viewing cos2(t) + sin2(t) = 1by Walter VanniniTriangles Unit Circle Root Mean Square Rotation Matrix Determinant Orthonormal Basis Combinatorial Identities Exponential Function Algebra Factorization Parametrized Curve Derivatives Integral Conservation Of Energy Hyperbolic Analogues Feedback IntroductionWe will explore various interpretations of the above identity. Later parts of this essay don't often depend on earlier parts, so please feel free to skim past incomprehensible text until you find something you're comfortable with. TrianglesThe usual way the identity is understood is via Pythagoras' theorem. In a right angled triangle with sides a,b,c, and angle t at the vertex where a and c meet, cos(t) is by definition a/c, sin(t) is by definition b/c , and so cos2(t) + sin2(t) is (a/c)2+(b/c)2, which by simple algebraic manipulation is (a2+b2)/c2. Pythagoras' theorem states that a2+b2 is c2, and so this simplifies to 1. 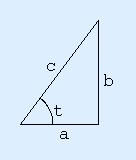 Unit CircleTraditionally (ie. the way I learned it), the next step is to realize that the unit circle centered at (0,0) in the (x,y) plane is defined by x2+y2=1. The above identity can then be interpreted as saying that the point (cos(t), sin(t)) is on the unit circle. Furthermore, this approach leads to a definition of cos(t) and sin(t) for all real t. 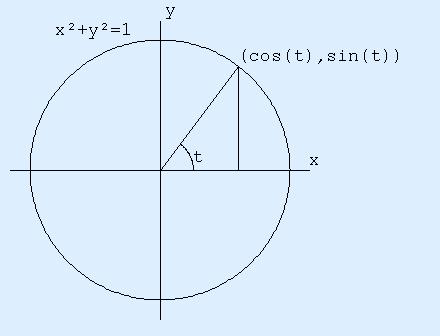 Root Mean SquareAnother way to understand this identity is via the trigonometric identities
Incidentally, these identities pretty much leap out at you from looking at the graphs of y = cos2(x) and y = sin2(x). 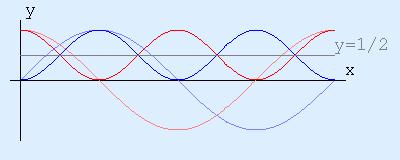
Another way to look at it is to remember that the root mean square of
cos is 1/√2, as is the root mean square of
sin. This means that cos2 is 1/2 +
variation, and sin2 is 1/2 +
variation, and amazingly the variation of
cos2 is precisely the negative of the variation of
sin2. Actually, this does fit in with the fact
that sin and cos are simply phase-shifted versions
of each other, so that sin2and
cos2 are phase-shifted versions of each other, so
their variations should be somehow related.
Rotation MatrixYet another way to understand the identity is via 2 by 2 matrices. The linear matrix that represents an anticlockwise rotation by angle t is
 DeterminantThe matrix
Orthonormal Basis
The rotation matrix sends the point (1,0) to
(cos(x),sin(x)) and the point (0,1) to (-sin(x),
cos(x)). The standard basis e1=(1,0),
e2=(0,1) is an orthonormal basis, meaning that
Since a rotation is a "rigid motion", it will transform an orthonormal basis to another orthonormal basis. This means that the above three equations will be true when e1 is (cos(t), sin(t)), and e2 is (-sin(t), cos(t)). The two equations e1.e1 = 1 and e2.e2 = 1 are each a restatement of cos2(t) + sin2(t) = 1, while e1.e2 = 0 is a statement of the identity cos(t)(-sin(t))+sin(t)cos(t) = 0. Strangely enough, even the e1.e2 statement is a manifestation of the identity, as is shown below. Combinatorial IdentitiesAnother way to look at the identity is via the power series expansions of cos(x) and sin(x).
This means that
In this context, the identity cos2(t)+sin2(t)=1 is really encoding an infinite number of identities involving factorials, namely
These identities can be reexpressed in terms of combinatorial coefficients ( nCr = n!/(n-r)!r!)
These are saying that the even combinatorial coefficients sum up to the same result as the odd combinatorial coefficients. This result can be proved directly. It is most easily seen by looking at Pascal's triangle, and adding the terms in a row in two different ways. Furthermore, using the power series expansions to extend the definition of cos and sin to the complex numbers, we now know that the identity is true for complex t. Thanks to Bob Uva for pointing this out. Exponential Function
Algebra
The first is to realize that the single equation eix =
cos(x)+isin(x) gives us the equation e-ix =
cos(x)-isin(x) and from these two equations we can solve for
cos(x) and sin(x) to get
FactorizationThe second is to be clever (in a different way), and realize we can factorize a2 + b2 as (a-ib)(a+ib). If you haven't seen this before, it's a restatement of a2-b2 = (a-b)(a+b). Using complex numbers, we have that -b2 is (ib)2, which leads to a2+b2 = a2-(-b2) = a2 - (ib)2 = (a-ib)(a+ib). Incidentally, it's of course also true that a2+b2 = (b-ia)(b+ia). Anyway, applying the factorization to cos2(x)+sin2(x), we get (cos(x)+isin(x))(cos(x)-isin(x)), which is eixe-ix. Using w to represent eix, the fact that cos2(x)+sin2(x)=1 is simply a convoluted way of saying w(1/w)=1. Parametrized Curve DerivativesConsider the parametrized curve c(t) = (cos(t), sin(t)). The identity tells us that this parametrized curve is always on the unit circle about the origin. Differentiating, we have c'(t) = (-sin(t), cos(t)) . c'(t).c'(t) is (-sin(t))(-sin(t)) + cos(t)cos(t), which is just cos2(t)+sin2(t). The fact that this is 1 tells us that the parametrized curve is actually parametrized by arc length. So, the trigonometric identity can be viewed as simply stating the fact that radians traverse the unit circle at unit speed. Finally, differentiating again, we get c''(t) = (-cos(t), -sin(t)). Obviously, c''(t).c''(t) = cos2(t) + sin2(t), so that the identity tells us that moving uniformly along the circle results in an acceleration of constant magnitude. IntegralFinally, another approach to establishing that cos2(x)+sin2(x) is 1 is to realize that it is really stating two separate properties, namely that cos2(x)+sin2(x) is a constant, and that the constant happens to be 1, ie. for some value of x, cos2(x)+sin2(x) is 1. The latter property is quickly established: taking x=0, cos(x)=1 and sin(x)= 0. Clearly 12+02 =1.
Given a function f, to establish that f is a
constant function, it suffices to establish that the derivative of
f is zero. Applying this technique to
f=cos2+sin2, the first step is using
the chain rule to get that the derivative of
cos2(x)+sin2(x) is 2cos(x)cos'x +
2sin(x)sin'(x). Via the derivative identities cos'(x) =
-sin(x), and sin'(x) = cos(x), we have that
2cos(x)cos'x + 2sin(x)sin'(x)simplifies to
2cos(x)(-sin(x)) + 2sin(x)cos(x) , which is zero. So the
identity can be viewed as the integrated version of the trivial
identity
Conservation Of EnergyYet another way to see that the cos2+sin2 is constant is to realize that it represents the sum of the potential and kinetic energies of the solution x=cos(t) to the equation for simple harmonic motion x''(t)+x(t)=0. For a particle of mass 1, the kinetic energy is (1/2)x'(t)2, and the potential energy is (1/2)x(t)2 (upto an additive constant). Conservation of energy tells us that (1/2)x'(t)2+(1/2)x(t)2 is a constant, and so x'(t)2+x(t)2 is also a constant. Taking the solution x(t)=cos(t) (or x(t)=sin(t)) we get the identity. I should mention that none of the above mathematics is dependent on the underlying physics. If x(t) is a solution to the second order equation x''(t)+F(x(t)) = 0, then (1/2)x'(t)2 + V(x(t)), where V is an antiderivative of F, is constant. Simple differentiation extablishes this.
Incidentally, since x(t)=acos(t)+bsin(t) is the general solution
to the second order equation, we have that Hyperbolic AnaloguesThe next step to understanding the identity is to compare and contrast it to the identity for hyperbolic cosine and hyperbolic sine, namely cosh2(t) - sinh2(t) = 1. I'll defer this to a later essay. FeedbackIf you have corrections, additions, modifications, etc please let me know mailto:walterv@gbbservices.com
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||